Afiliacja: Uniwersytet im. A. Mickiewicza w Poznaniu
W tym miesiącu w Kąciku Początkującego Olimpijczyka (patrz ostatnia strona Delty) kontynuujemy temat skojarzeń w grafach. Są z nim związane dwa ważne twierdzenia: Tutte’a i Halla. Ich uzasadnienia są bardzo pouczające, a ponieważ nie udałoby mi się ich zmieścić na ostatniej stronie, przedstawiam je w niniejszym artykule, Kącikowi pozostawiając same zadania z rozwiązaniami.
Przed przystąpieniem do lektury zachęcamy Czytelnika do zapoznania się z Kącikiem Początkującego Olimpijczyka nr 68 i 69 w \(\Delta_{24}^8\) i \(\Delta_{24}^9\). Są tam wszystkie niezbędne definicje.
Zaczniemy od podstawowego narzędzia. Niech \(M\) będzie skojarzeniem w grafie \(G.\) Ścieżkę nazywamy naprzemienną dla skojarzenia \(M,\) jeśli ma krawędzie na zmianę nienależące i należące do \(M.\)
Lemat o ścieżce naprzemiennej. Jeśli istnieje ścieżka naprzemienna łącząca pewne dwa wierzchołki grafu \(G\) nienależące do skojarzenia \(M,\) to skojarzenie \(M\) nie jest największe.
Dowód: Niech \(P\) będzie opisaną w lemacie ścieżką naprzemienną. Ze skojarzenia \(M\) usuńmy te krawędzie, które należą do \(P\) i zamiast tego dołączmy te krawędzie \(P,\) które nie były wcześniej w \(M.\) W ten sposób otrzymujemy podgraf \(M',\) który ma o jedną krawędź więcej niż \(M.\)
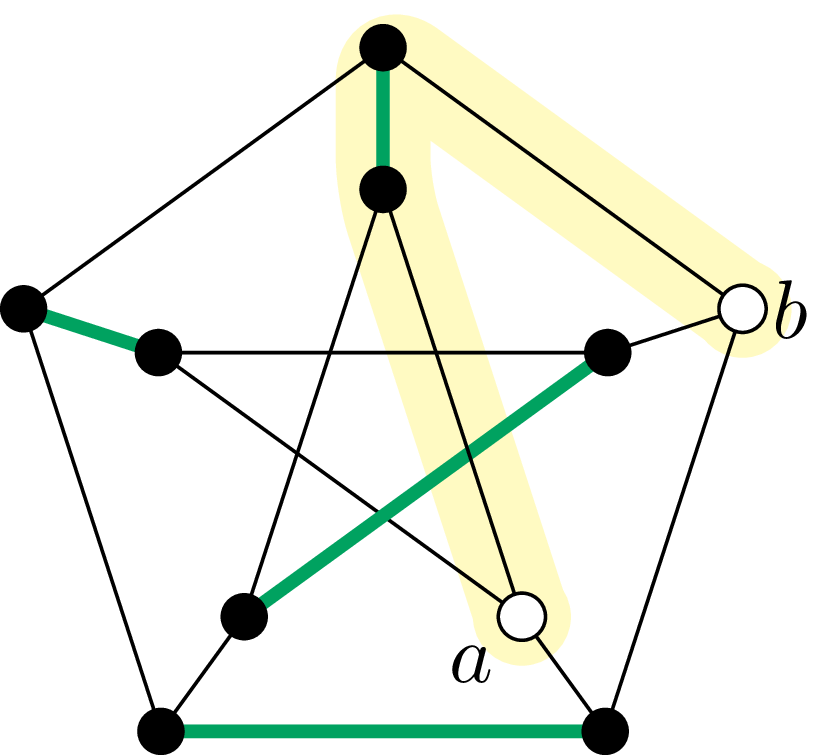
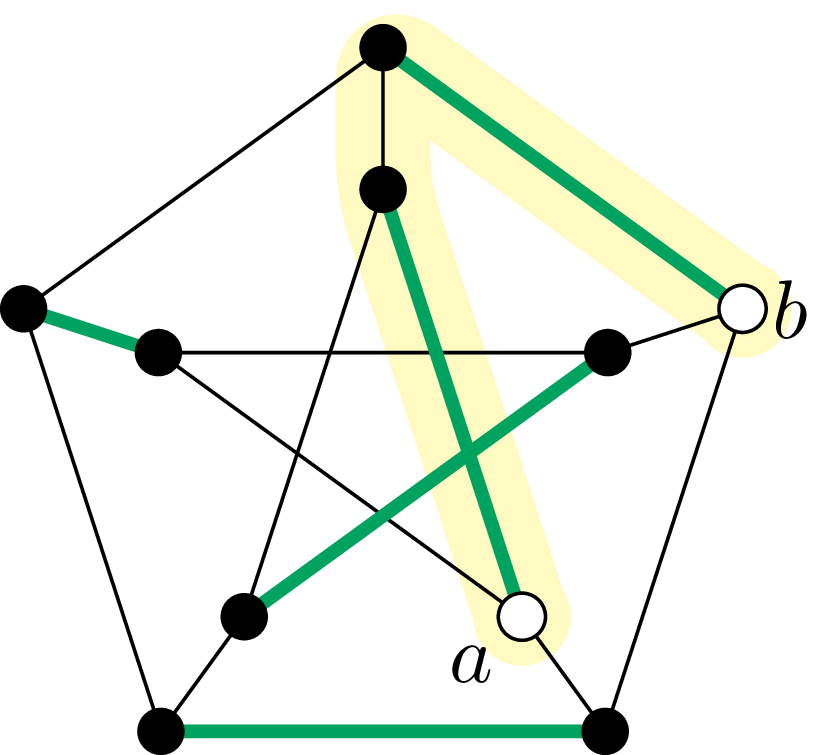
Ścieżka \(P\) została podświetlona na żółto. Na rysunku z lewej pogrubione zielone krawędzie należą do \(M,\) a z prawej – do \(M'\)
Ten podgraf jest nadal skojarzeniem, gdyż w wyniku przeprowadzonej powyżej operacji stopnie wierzchołków \(a\) i \(b\) wzrosły z \(0\) do \(1,\) a pozostałe nie zmieniły się. \(\square\)
Ścieżka opisana w lemacie nazywana jest często ścieżką powiększającą skojarzenie.
Wprowadźmy teraz definicje potrzebne do sformułowania twierdzenia Tutte’a.
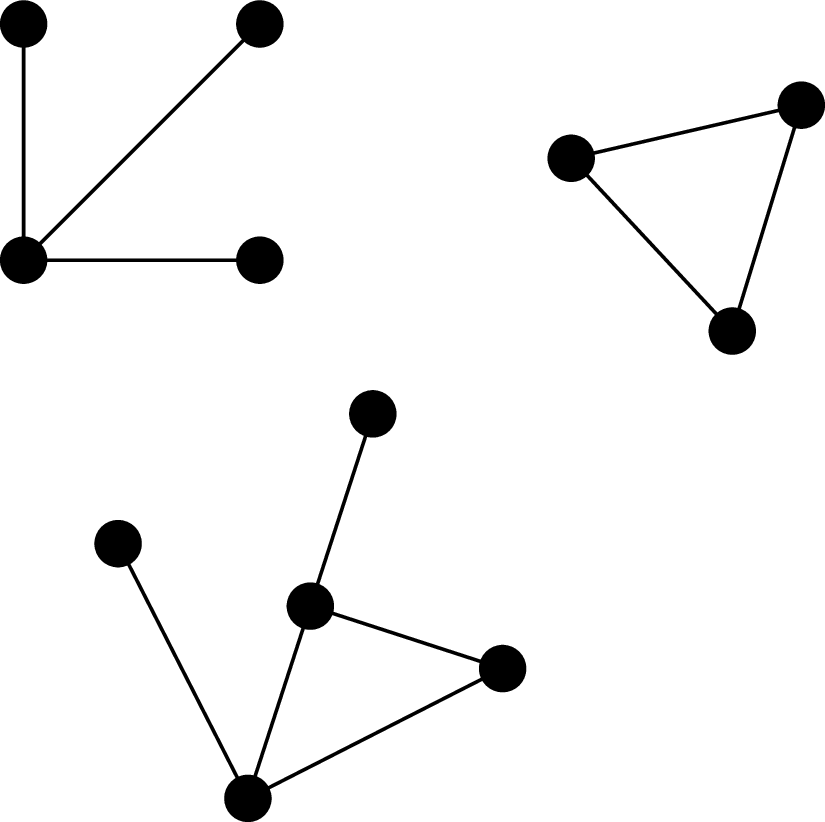
Powyższy graf \(G\) ma trzy spójne składowe, z czego dwie mają nieparzystą liczbę wierzchołków, zatem \(\mathcal{O}(G)=2\)
Graf nazywamy spójnym, jeśli każde dwa jego wierzchołki połączone są ścieżką. Każdy maksymalny (w sensie relacji bycia podgrafem) podgraf spójny danego grafu nazywamy jego spójną składową. Spójne składowe o parzystej liczbie wierzchołków będziemy nazywać parzystymi, a o nieparzystej – nieparzystymi. Oznaczmy przez \(\mathcal{O}(G)\) liczbę nieparzystych spójnych składowych grafu \(G.\)
Niech \(G=(V,E)\) będzie grafem i niech \(S\subsetneq V.\) Przez \(G-S\) rozumiemy graf \(G\) z usuniętymi wszystkimi wierzchołkami należącymi do \(S\) oraz usuniętymi wszystkimi krawędziami, które mają co najmniej jeden koniec w zbiorze \(S.\)
Twierdzenie Tutte’a. Graf \(G=(V,E)\) ma skojarzenie pełne wtedy i tylko wtedy, gdy \[\label{KPO-Tutte}\tag{T} \mathop{\forall}_{S\subsetneq V} \mathcal{O}(G-S)\le|S|.\]
Zbiory \(S\) spełniające warunek \(\mathcal{O}(G-S)\le|S|\) będziemy nazywać dobrymi, a niespełniające go – niedobrymi. Zwróćmy uwagę, że odrzucamy tu \(S=V\) (wtedy \(G-S\) nie jest grafem, choć nawet jeśli dopuścimy graf pusty, to ma on 0 składowych nieparzystych), ale uwzględniony jest zbiór pusty. Dla \(S=\emptyset\) otrzymujemy w warunku \(\eqref{KPO-Tutte}\), że \(\mathcal{O}(G)=0,\) czyli każda spójna składowa grafu \(G\) jest parzysta. Jest to oczywisty warunek konieczny istnienia skojarzenia pełnego.
Dowód (\(\Rightarrow\)). Zakładamy, że graf \(G=(V,E)\) ma skojarzenie pełne. Należy wykazać, że każdy zbiór \(S\subsetneq V\) jest dobry. Dla \(S=\emptyset\) już to zrobiliśmy, niech więc \(|S|\ge1.\) Każda nieparzysta spójna składowa grafu \(G-S\) ma przynajmniej jeden wierzchołek, który jest skojarzony z wierzchołkiem spoza niej. Nie może on należeć do innej spójnej składowej, więc musi należeć do zbioru \(S.\) Każdej spójnej składowej grafu \(G-S\) można w ten sposób przypisać pewien wierzchołek ze zbioru \(S.\) To przyporządkowanie jest różnowartościowe (bo idzie wzdłuż krawędzi skojarzenia), więc \(\mathcal{O}(G-S)\le|S|.\)
Dowód (\(\Leftarrow\)). Teraz zakładamy, że spełniony jest warunek \(\eqref{KPO-Tutte}\). Dla dowodu nie wprost dodatkowo przypuśćmy, że w grafie \(G\) nie ma skojarzenia pełnego. Wówczas graf \(G\) ma parzystą liczbę wierzchołków (warunek \(\eqref{KPO-Tutte}\) dla \(S=\emptyset\)) i nie jest grafem pełnym.
Niech \(G'=G+e\) będzie grafem \(G\) z dodaną krawędzią \(e.\) Graf \(G'\) nadal spełnia warunek \(\eqref{KPO-Tutte}\), ponieważ dla dowolnego \(S\subsetneq V\) zachodzi \(\mathcal{O}(G'-S)\leq\mathcal{O}(G-S).\) Istotnie, krawędź \(e\) może łączyć wierzchołki:
z których co najmniej jeden należy do \(S\);
z tej samej spójnej składowej grafu \(G-S\);
z różnych parzystych spójnych składowych grafu \(G-S\);
z parzystej i nieparzystej składowej grafu \(G-S\);
z różnych nieparzystych spójnych składowych grafu \(G-S.\)
W pierwszych czterech przypadkach mamy \(\mathcal{O}(G'-S)=\mathcal{O}(G-S),\) a w ostatnim \(\mathcal{O}(G'-S)=\mathcal{O}(G-S)-2.\) Możemy zatem przyjąć bez utraty ogólności, że dodanie jakiejkolwiek krawędzi spowoduje zaistnienie skojarzenia pełnego.
Niech \(U\) będzie zbiorem wszystkich wierzchołków grafu \(G\) o stopniu \(|V|-1,\) czyli wierzchołków połączonych z każdym innym. Wykażemy, że zbiór \(U\) jest niedobry, co będzie poszukiwaną sprzecznością.
Zauważmy najpierw, że nie wszystkie spójne składowe grafu \(G-U\) są klikami – inaczej graf \(G\) miałby skojarzenie pełne.
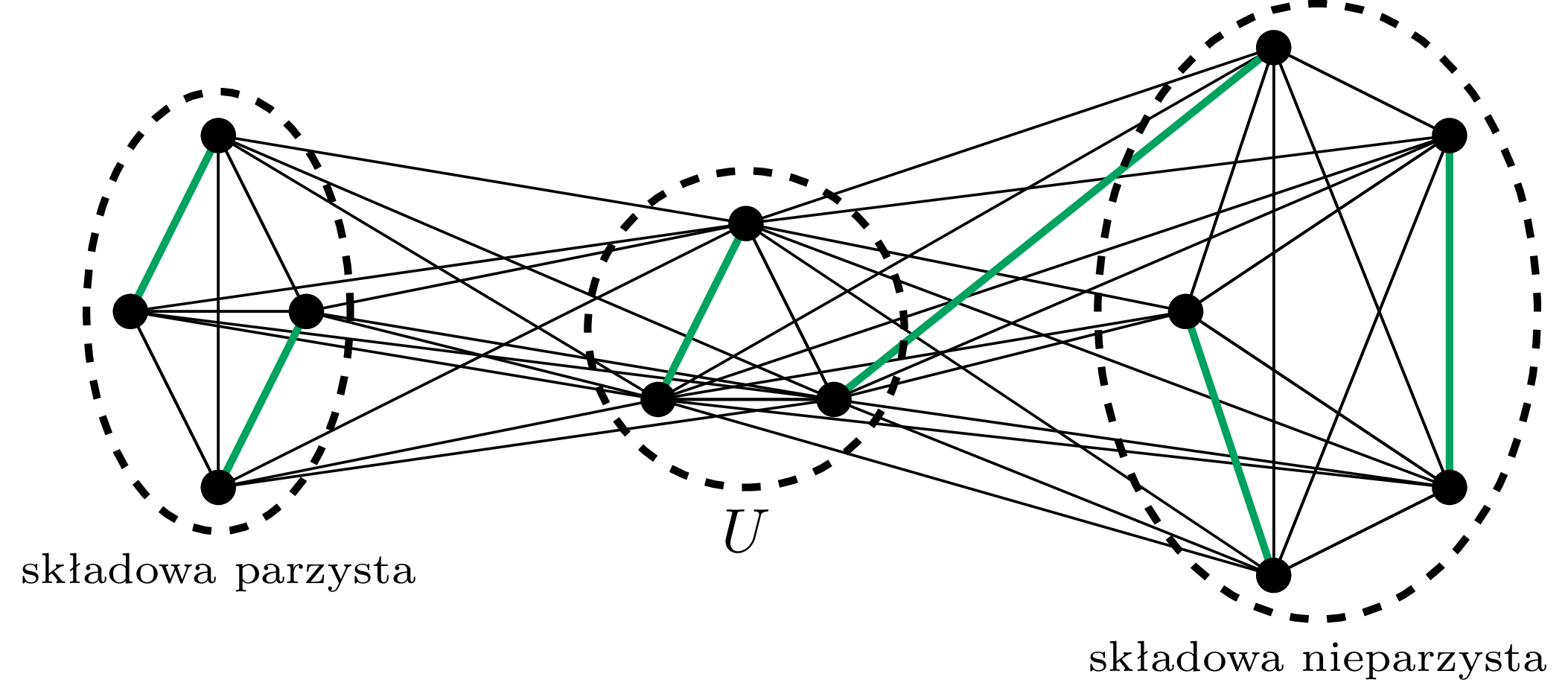
W każdej spójnej składowej można by było dowolnie połączyć w pary wszystkie wierzchołki oprócz najwyżej jednego. Niesparowanych wierzchołków w składowych jest dokładnie \(\mathcal{O}(G-U),\) więc możemy je połączyć z różnymi wierzchołkami ze zbioru \(U.\) Pozostałe wierzchołki ze zbioru \(U\) dowolnie łączymy w pary.
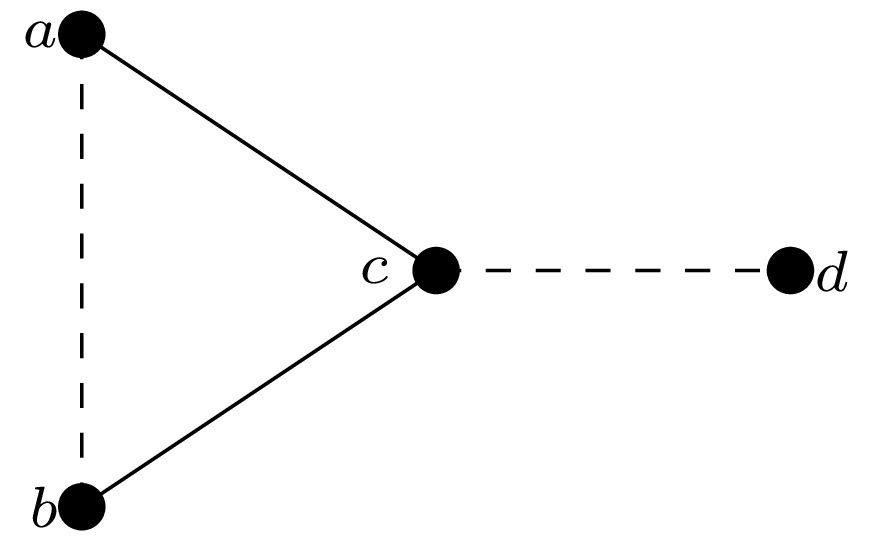
Teraz wykażemy, że w grafie \(G\) istnieje struktura widoczna na rysunku obok (linia przerywana oznacza tu brak sąsiedztwa). Niech \(S_0\) będzie spójną składową grafu \(G-U\) niebędącą kliką. Ma ona zatem dwa wierzchołki \(x\) i \(y,\) które nie są połączone krawędzią. Wierzchołki \(a,\) \(c,\) \(b\) wybieramy jako trzy kolejne na najkrótszej ścieżce łączącej \(x\) i \(y.\) Ponadto \(c\not\in U,\) więc istnieje wierzchołek \(d\in V,\) z którym \(c\) nie jest połączony.
Wobec poczynionych wcześniej założeń, w grafie \(G+ab\) znajdziemy pewne skojarzenie pełne \(M_1,\) a w grafie \(G+cd\) – skojarzenie pełne \(M_2.\) Ponieważ w \(G\) nie było skojarzenia pełnego, więc krawędź \(ab\) należy do skojarzenia \(M_1,\) a \(cd\) – do \(M_2.\) Skojarzenie \(M_1-\{a,b\}\) ma o jedną krawędź mniej niż miałoby skojarzenie pełne w grafie \(G,\) analogicznie skojarzenie \(M_2-\{c,d\}.\) Wystarczy zatem znaleźć ścieżkę powiększającą któreś z tych skojarzeń.
Przypominamy, że odejmując \(\{v,w\},\) usuwamy wierzchołki \(v,w\) i wszystkie krawędzie mające co najmniej jeden koniec w \(v\) lub \(w.\)
Sumą skojarzeń \(M_1\) i \(M_2\) jest multigraf \(H,\) w którym wszystkie wierzchołki są stopnia \(2.\) Taki multigraf jest sumą parami rozłącznych cykli, być może o długości \(2.\) W każdym takim cyklu krawędzie z \(M_1\) i \(M_2\) występują na przemian.
Multigraf to graf, w którym dopuszczamy wielokrotne krawędzie, na przykład jak ten poniżej.
Jeśli krawędzie \(ab\) i \(cd\) leżą na rozłącznych cyklach, odpowiednio \(C_1\) i
\(C_2,\) to ścieżka \(C_1-ab\) powiększa skojarzenie \(M_1-\{a,b\}\) w grafie \(G.\)
Pozostaje przypadek, gdy
\(ab\) i \(cd\) leżą na jednym cyklu. Możemy przyjąć, że wierzchołki \(a,\) \(b,\) \(c,\) \(d\) leżą na tym cyklu w tejże kolejności.
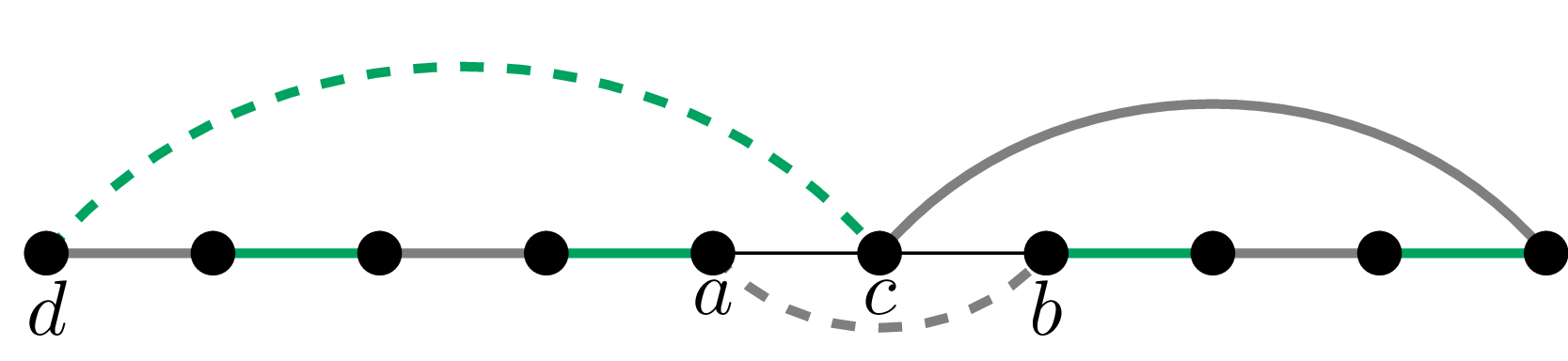 Wówczas ścieżka od \(c\) do \(d\) powiększa skojarzenie \(M_2-\{c,d\}\) w grafie \(G.\)
\(\square\)
Wówczas ścieżka od \(c\) do \(d\) powiększa skojarzenie \(M_2-\{c,d\}\) w grafie \(G.\)
\(\square\)
Można powiedzieć, że twierdzenie Tutte’a pozwala stwierdzić, czy w danej klasie, w której wiadomo, kto z kim się lubi, możemy usadzić uczniów w ławkach w taki sposób, że każdy siedzi z kimś, kogo lubi. A co, jeśli dodatkowo chcemy, by w każdej ławce siedzieli chłopiec i dziewczynka? Tu wygodnego kryterium dostarcza twierdzenie Halla, które omawiamy poniżej.
Ale najpierw potrzebne definicje. Grafem dwudzielnym o dwupodziale \((A,B)\) nazywamy taki graf, w którym zbiór wierzchołków jest sumą rozłącznych zbiorów \(A\) i \(B,\) ponadto każda krawędź ma jeden koniec w \(A,\) a drugi w \(B.\) Mówimy, że skojarzenie \(M\) nasyca zbiór \(A,\) jeśli każdy wierzchołek ze zbioru \(A\) należy do \(M.\)
Niech \(G=(V,E)\) będzie grafem i niech \(U\subseteq V.\) Sąsiedztwem zbioru \(U\) nazywamy zbiór tych wierzchołków spoza \(U,\) które mają co najmniej jednego sąsiada w \(U.\) Oznaczamy je przez \(N_G(U).\) Jeśli jest oczywiste, o jaki graf chodzi, to można pisać po prostu \(N(U).\)
Twierdzenie Halla. Graf dwudzielny \(G\) o dwupodziale \((A,B)\) ma skojarzenie nasycające zbiór \(A\) wtedy i tylko wtedy, gdy
\[\label{KPO-Hall}\tag{H}
\mathop{\forall}_{S\subseteq A} |N_G(S)|\ge|S|.\]
Dowód (\(\Rightarrow\)). Załóżmy, że graf ma skojarzenie \(M\) nasycające zbiór \(A.\) Niech \(S={s_1,s_2,\ldots,s_m}\subseteq A\) będzie dowolny. Przez \(s_i'\in B\) oznaczmy unikalnego sąsiada wierzchołka \(s_i\) w skojarzeniu \(M.\)
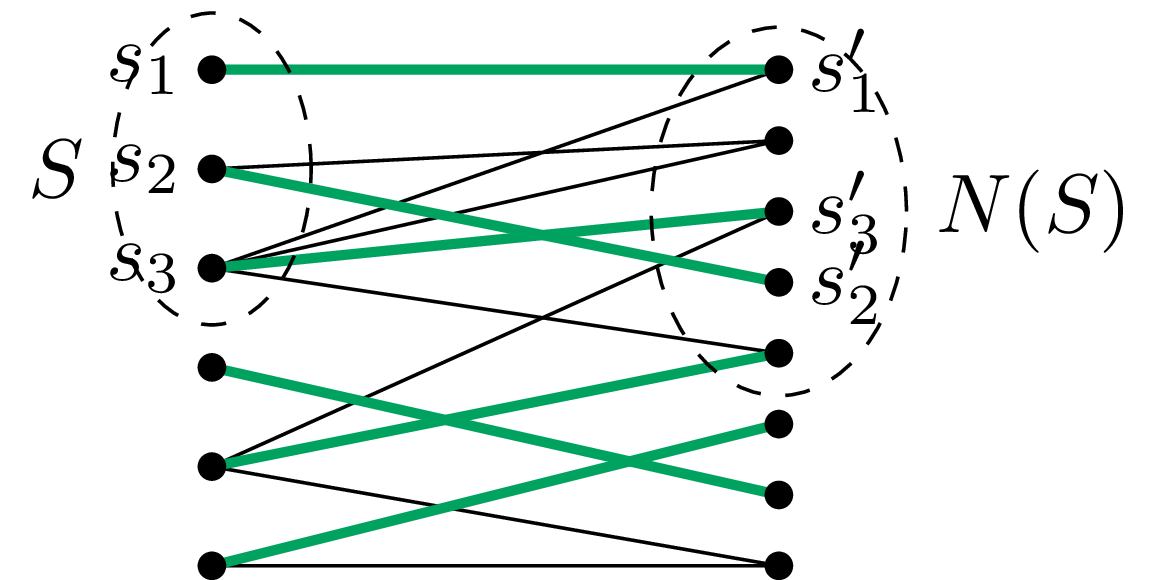 Wówczas \(s_1',s_2',\ldots,s_m'\in N(S)\) są różne, więc \({|N(S)|\ge m = |S|}.\)
Wówczas \(s_1',s_2',\ldots,s_m'\in N(S)\) są różne, więc \({|N(S)|\ge m = |S|}.\)
Dowód (\(\Leftarrow\)). Niech \(M\) będzie największym skojarzeniem w grafie \(G.\) Przypuśćmy, że skojarzenie \(M\) nie nasyca zbioru \(A.\) Udowodnimy, że warunek \(\eqref{KPO-Hall}\) nie jest wtedy spełniony.
Na mocy przypuszczenia nie wprost, pewien wierzchołek \(a\in A\) nie należy do skojarzenia \(M.\) Rozważmy wszystkie wierzchołki grafu \(G\) połączone z wierzchołkiem \(a\) za pomocą ścieżek naprzemiennych dla skojarzenia \(M.\) Niech \(S\) oznacza tę część spośród wspomnianych wierzchołków, która należy do zbioru \(A,\) razem z wierzchołkiem \(a,\) natomiast \(T\) – tę część, która jest w zbiorze \(B.\)
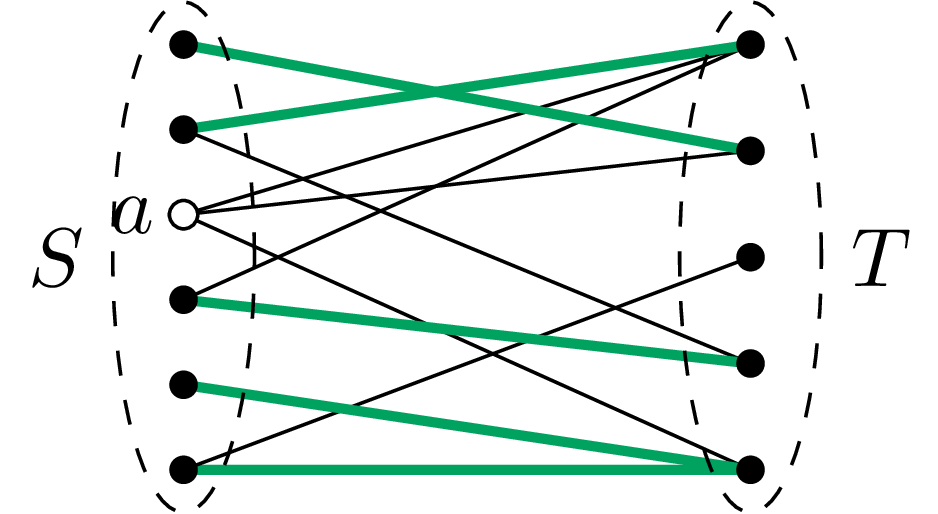 Każda ścieżka naprzemienna rozpoczęta w wierzchołku \(a\) i zakończona w wierzchołku należącym do \(T\) może być kontynuowana – w przeciwnym
razie otrzymalibyśmy ścieżkę powiększającą skojarzenie \(M.\)
W takim razie z każdym wierzchołkiem \(t\in T\) możemy
związać wierzchołek \(s\in S,\) który pojawia się bezpośrednio po \(t\) na pewnej ścieżce naprzemiennej,
startującej z \(a.\) Wierzchołek \(s\) jest wyznaczony jednoznacznie, gdyż krawędź
\(ts\) należy do skojarzenia \(M\) (a w skojarzeniu nie mogą pojawić się krawędzie
\(ts\) i \(ts'\) dla \(s\neq s'\)). Dokładnie tak samo uzasadniamy, że różnym
wierzchołkom z \(T\) odpowiadają różne wierzchołki z \(S,\) i że są one
różne od \(a.\) Dowodzimy w ten sposób, że \(|S|>|T|.\)
Każda ścieżka naprzemienna rozpoczęta w wierzchołku \(a\) i zakończona w wierzchołku należącym do \(T\) może być kontynuowana – w przeciwnym
razie otrzymalibyśmy ścieżkę powiększającą skojarzenie \(M.\)
W takim razie z każdym wierzchołkiem \(t\in T\) możemy
związać wierzchołek \(s\in S,\) który pojawia się bezpośrednio po \(t\) na pewnej ścieżce naprzemiennej,
startującej z \(a.\) Wierzchołek \(s\) jest wyznaczony jednoznacznie, gdyż krawędź
\(ts\) należy do skojarzenia \(M\) (a w skojarzeniu nie mogą pojawić się krawędzie
\(ts\) i \(ts'\) dla \(s\neq s'\)). Dokładnie tak samo uzasadniamy, że różnym
wierzchołkom z \(T\) odpowiadają różne wierzchołki z \(S,\) i że są one
różne od \(a.\) Dowodzimy w ten sposób, że \(|S|>|T|.\)
Jest jasne, że \(T\subseteq N(S).\) Wykażemy, że zachodzi tu równość. Niech \(w\in N(S)\) – wtedy ma on sąsiada \(s\in S,\) więc albo \(s=a\) (i wtedy \(w\in T\)), albo istnieje ścieżka naprzemienna \(P\) o kolejnych wierzchołkach \(a,\ldots,t,s.\) Krawędź \(ts\) należy do skojarzenia \(M,\) więc krawędź \(sw\) nie może do niego należeć. Wobec tego ścieżka o kolejnych wierzchołkach \(a,\ldots,t,s,w\) jest naprzemienna i w konsekwencji \(w\in T.\)
Wobec powyższych rozważań \(|S|>|T|=|N(S)|\) i warunek \(\eqref{KPO-Hall}\) nie jest spełniony, co kończy dowód. \(\square\)
Przykłady zastosowań oraz zadania Czytelnik znajdzie na ostatniej stronie niniejszego numeru Delty.